Trigonometric Substitutions Trigonometric Substitutions Trigonometric Substitutions This page is dedicated to teaching problem solving techniques, specifically for trigonometric substitution. For other integration methods see other sources.
The format is aimed at first introducing the theory, the techniques, the steps and finally a series of examples which will make you further skilled.
Basic Differentiation
Basic Integration Methods
Pythagoras Theorem This area is covered by the wikipedia article W:Trigonometric substitution and the wikibooks module B:Calculus/Integration techniques/Trigonometric Substitution . On this page we deal with the practical aspects.
Trigonometric substitution is a special case of simplifying an intergrand which has a specific form. We will first outline these forms and where they came from.
We should be familiar with pythagoras theorem for a right angled triangle.
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
From this familiar definition we can derive other definitions. eg.
c
=
a
2
+
b
2
.
{\displaystyle c={\sqrt {a^{2}+b^{2}}}.\,}
By expanding upon this theory we can come up with other relationships which help us with integration.
(
sin
θ
)
=
a
2
−
x
2
x
=
a
sin
θ
a
2
cos
2
(
θ
)
{\displaystyle (\sin \theta )={\sqrt {a^{2}-x^{2}}}\qquad x=a\sin \theta \qquad {\sqrt {a^{2}\cos ^{2}(\theta )}}\,}
From the diagram
sin
θ
=
opposite
hypotenuse
=
x
a
{\displaystyle \sin \theta ={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {x}{a}}}
(
sin
θ
)
2
+
x
2
=
a
2
{\displaystyle (\sin \theta )^{2}+x^{2}=a^{2}\,}
(
sin
θ
)
2
=
a
2
−
x
2
{\displaystyle (\sin \theta )^{2}=a^{2}-x^{2}\,}
(
sin
θ
)
=
a
2
−
x
2
{\displaystyle (\sin \theta )={\sqrt {a^{2}-x^{2}}}\,}
x
=
a
sin
θ
{\displaystyle x=a\sin \theta \,}
a
2
−
x
2
{\displaystyle {\sqrt {a^{2}-x^{2}}}\,}
a
2
−
(
a
sin
θ
)
2
{\displaystyle {\sqrt {a^{2}-(a\sin \theta )^{2}}}\,}
a
2
−
(
a
2
sin
2
(
θ
)
)
{\displaystyle {\sqrt {a^{2}-(a^{2}\sin ^{2}(\theta ))}}\,}
a
2
(
1
−
sin
2
(
θ
)
)
{\displaystyle {\sqrt {a^{2}(1-\sin ^{2}(\theta ))}}\,}
cos
2
(
θ
)
=
1
−
sin
2
(
θ
)
{\displaystyle \cos ^{2}(\theta )=1-\sin ^{2}(\theta )\,}
a
2
cos
2
(
θ
)
{\displaystyle {\sqrt {a^{2}\cos ^{2}(\theta )}}\,}
(
tan
θ
)
=
a
2
+
x
2
x
=
a
tan
θ
{\displaystyle (\tan \theta )={\sqrt {a^{2}+x^{2}}}\qquad x=a\tan \theta \,}
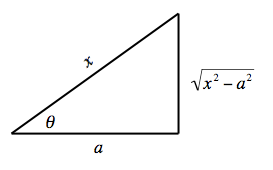
(
sec
θ
)
=
x
2
−
a
2
x
=
a
sec
θ
{\displaystyle (\sec \theta )={\sqrt {x^{2}-a^{2}}}\qquad x=a\sec \theta \,}
From the diagram
cos
θ
=
adjacent
hypotenuse
=
a
x
{\displaystyle \cos \theta ={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {a}{x}}}
sec
θ
=
1
cos
θ
{\displaystyle \sec \theta ={\frac {1}{\cos \theta }}}
sec
θ
=
hypotenuse
adjacent
=
x
a
{\displaystyle \sec \theta ={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {x}{a}}}
(
sec
θ
)
2
+
a
2
=
x
2
{\displaystyle (\sec \theta )^{2}+a^{2}=x^{2}\,}
(
sec
θ
)
2
=
x
2
−
a
2
{\displaystyle (\sec \theta )^{2}=x^{2}-a^{2}\,}
(
sec
θ
)
=
x
2
−
a
2
{\displaystyle (\sec \theta )={\sqrt {x^{2}-a^{2}}}\,}
x
=
a
sec
θ
{\displaystyle x=a\sec \theta \,}
x
2
−
a
2
{\displaystyle {\sqrt {x^{2}-a^{2}}}\,}
(
a
sec
θ
)
2
−
a
2
{\displaystyle {\sqrt {(a\sec \theta )^{2}-a^{2}}}\,}
(
a
2
sec
2
θ
)
−
a
2
{\displaystyle {\sqrt {(a^{2}\sec ^{2}\theta )-a^{2}}}\,}
a
2
(
sec
2
(
θ
)
−
1
)
{\displaystyle {\sqrt {a^{2}(\sec ^{2}(\theta )-1)}}\,}
sec
2
(
θ
)
−
1
=
tan
2
(
θ
)
{\displaystyle \sec ^{2}(\theta )-1=\tan ^{2}(\theta )\,}
a
2
tan
2
(
θ
)
{\displaystyle {\sqrt {a^{2}\tan ^{2}(\theta )}}\,}
Definition 1 Sine
Definition 2 Tan
Definition 3 Sec
(
sin
θ
)
=
a
2
−
x
2
{\displaystyle (\sin \theta )={\sqrt {a^{2}-x^{2}}}\,}
(
tan
θ
)
=
a
2
+
x
2
{\displaystyle (\tan \theta )={\sqrt {a^{2}+x^{2}}}\,}
(
sec
θ
)
=
x
2
−
a
2
{\displaystyle (\sec \theta )={\sqrt {x^{2}-a^{2}}}\,}
This table summarises the definitions that we identify in special integral cases and how they relate to trig identities.
We begin with the integral
∫
d
x
a
2
−
x
2
{\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}}
Step 1 - Identify Trigonometric Substitution Type
Step 2 - Identifying Identities for Substitution
x
=
a
sin
(
θ
)
{\displaystyle x=a\sin(\theta )\,}
Step 3 - Substituting Identities into Integral
∫
d
x
a
2
−
x
2
{\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}}
=
∫
a
cos
(
θ
)
a
2
−
a
2
sin
2
(
θ
)
d
θ
substituting
x
=
a
sin
(
θ
)
and
d
x
=
a
cos
(
θ
)
d
θ
{\displaystyle =\int {\frac {a\cos(\theta )\,}{\sqrt {a^{2}-a^{2}\sin ^{2}(\theta )}}}\ d\theta \qquad {\textrm {substituting}}\qquad x=a\sin(\theta )\qquad {\textrm {and}}\qquad dx=a\cos(\theta )\,d\theta }
=
∫
a
cos
(
θ
)
a
2
(
1
−
sin
2
(
θ
)
)
d
θ
{\displaystyle =\int {\frac {a\cos(\theta )\,}{\sqrt {a^{2}(1-\sin ^{2}(\theta ))}}}\ d\theta }
=
∫
a
cos
(
θ
)
a
2
cos
2
(
θ
)
d
θ
{\displaystyle =\int {\frac {a\cos(\theta )\,}{\sqrt {a^{2}\cos ^{2}(\theta )}}}\ d\theta }
=
∫
a
cos
(
θ
)
a
cos
(
θ
)
d
θ
{\displaystyle =\int {\frac {a\cos(\theta )\,}{a\cos(\theta )}}\ d\theta }
=
∫
d
θ
{\displaystyle =\int d\theta \,}
=
θ
+
C
{\displaystyle =\theta +C\,}
Step 5 - Final Substitution of
θ
{\displaystyle \theta \,}
the question is in terms of
x
so we need the final substitution
θ
=
arcsin
(
x
a
)
or
θ
=
sin
−
1
(
x
a
)
{\displaystyle {\text{the question is in terms of }}x{\text{ so we need the final substitution}}\qquad \theta =\arcsin \left({\frac {x}{a}}\right){\text{ or }}\theta =\sin ^{-1}\left({\frac {x}{a}}\right)}
=
arcsin
(
x
a
)
+
C
or
{\displaystyle =\arcsin \left({\frac {x}{a}}\right)+C\,\qquad {\text{or}}}
=
sin
−
1
(
x
a
)
+
C
{\displaystyle =\sin ^{-1}\left({\frac {x}{a}}\right)+C\,}
Evaluate
∫
x
2
−
25
x
d
x
{\displaystyle \int {\frac {\sqrt {x^{2}-25}}{x}}dx\,}
Solution
In a formal solution there are typically more parts than outlined in the technique section, but the steps remain the same.
{\displaystyle {\text{In a formal solution there are typically more parts than outlined in the technique section, but the steps remain the same.}}\,}
Step 1 - Identify Trigonometric Substitution Type
We look at the format for the square root and recognise it as being a sec substitution.
{\displaystyle {\text{We look at the format for the square root and recognise it as being a sec substitution.}}\,}
Step 2 - Identifying Identities for Substitution
x
=
5
sec
θ
.
{\displaystyle x=5\sec \theta \,.}
x
{\displaystyle x\,}
x
2
−
a
2
{\displaystyle x^{2}-a^{2}\,}
d
x
{\displaystyle dx\,}
θ
{\displaystyle \theta \,}
tan
θ
{\displaystyle \tan \theta \,}
x
=
a
sec
(
θ
)
{\displaystyle x=a\sec(\theta )\,}
x
2
−
5
2
=
(
5
sec
θ
)
2
−
25
{\displaystyle x^{2}-5^{2}=(5\sec \theta )^{2}-25\,}
x
=
5
sec
(
θ
)
{\displaystyle x=5\sec(\theta )\,}
x
=
5
sec
(
θ
)
{\displaystyle x=5\sec(\theta )\,}
x
2
−
25
=
25
tan
2
θ
{\displaystyle x^{2}-25=25\tan ^{2}\theta \,}
x
=
5
sec
(
θ
)
{\displaystyle x=5\sec(\theta )\,}
=
25
(
sec
2
θ
−
1
)
{\displaystyle =25(\sec ^{2}\theta -1)\,}
d
x
d
θ
=
5
sec
tan
(
θ
)
{\displaystyle {\frac {dx}{d\theta }}=5\sec \tan(\theta )}
sec
(
θ
)
=
x
5
{\displaystyle \sec(\theta )={\frac {x}{5}}}
solve for
tan
θ
{\displaystyle {\text{solve for }}\tan \theta \,}
tan
2
θ
=
x
2
−
25
25
{\displaystyle \tan ^{2}\theta \ ={\frac {x^{2}-25}{25}}}
=
25
tan
2
θ
{\displaystyle =25\tan ^{2}\theta \,}
d
x
=
5
sec
tan
(
θ
)
d
θ
{\displaystyle dx=5\sec \tan(\theta )\,d\theta }
θ
=
arcsec
(
x
5
)
{\displaystyle \theta =\operatorname {arcsec} \left({\frac {x}{5}}\right)}
or
θ
=
sec
−
1
(
x
5
)
{\displaystyle \theta =\sec ^{-1}\left({\frac {x}{5}}\right)}
tan
θ
=
x
2
−
25
5
{\displaystyle \tan \theta \ ={\frac {\sqrt {x^{2}-25}}{5}}\,}
x
{\displaystyle x\,}
x
=
a
sec
θ
. In this case
a
=
25
=
5
thus
x
=
5
sec
θ
.
{\displaystyle x=a\sec \theta {\text{. In this case }}a={\sqrt {25}}=5\,{\text{ thus }}x=5\sec \theta \,.}
x
2
−
a
2
{\displaystyle x^{2}-a^{2}\,}
x
2
−
25
=
25
tan
2
θ
{\displaystyle x^{2}-25=25\tan ^{2}\theta \,}
x
2
−
25
=
(
5
sec
θ
)
2
−
25
{\displaystyle x^{2}-25=(5\sec \theta )^{2}-25\,}
=
25
(
sec
2
θ
−
1
)
{\displaystyle =25(\sec ^{2}\theta -1)\,}
=
25
tan
2
θ
{\displaystyle =25\tan ^{2}\theta \,}
d
x
{\displaystyle dx\,}
d
x
=
5
sec
tan
θ
d
θ
{\displaystyle dx=5\sec \tan \theta d\theta \,}
d
x
d
θ
=
5
sec
tan
θ
{\displaystyle {\frac {dx}{d\theta }}=5\sec \tan \theta }
NOTE: For differentiating
x
=
5
sec
θ
{\displaystyle {\text{NOTE: For differentiating }}x=5\sec \theta \,}
x
=
5
sec
θ
=
5
1
cos
θ
=
5
cos
θ
{\displaystyle x=5\sec \theta \,\qquad =5{\frac {1}{\cos \theta }}\qquad ={\frac {5}{\cos \theta }}\,}
d
d
θ
=
v
u
′
−
u
v
′
v
2
using Quotient Rule
{\displaystyle {\frac {d}{d\theta }}={\frac {vu'-uv'}{v^{2}}}\qquad {\text{using Quotient Rule}}}
=
cos
θ
.0
−
5.
(
−
sin
θ
)
cos
2
θ
=
5
sin
θ
cos
2
θ
=
5
cos
θ
.
sin
θ
cos
θ
=
5
sec
θ
tan
θ
{\displaystyle \qquad ={\frac {\cos \theta .0-5.(-\sin \theta )}{\cos ^{2}\theta }}\qquad ={\frac {5\sin \theta }{\cos ^{2}\theta }}\qquad ={\frac {5}{\cos \theta }}.{\frac {\sin \theta }{\cos \theta }}=5\sec \theta \tan \theta }
Values for
θ
{\displaystyle {\text{Values for }}\theta \,}
tan
θ
=
x
2
−
25
5
,
{\displaystyle \tan \theta \ ={\frac {\sqrt {x^{2}-25}}{5}},}
recall
x
2
−
25
=
25
tan
2
θ
{\displaystyle {\text{recall }}x^{2}-25=25\tan ^{2}\theta \,}
solve for
tan
θ
{\displaystyle {\text{solve for }}\tan \theta \,}
tan
2
θ
=
x
2
−
25
25
{\displaystyle \tan ^{2}\theta \ ={\frac {x^{2}-25}{25}}\,}
tan
θ
=
x
2
−
25
5
{\displaystyle \tan \theta \ ={\frac {\sqrt {x^{2}-25}}{5}}\,}
θ
=
sec
−
1
x
5
{\displaystyle \theta =\sec ^{-1}{\frac {x}{5}}\,}
recall
x
=
5
sec
θ
{\displaystyle {\text{recall }}x=5\sec \theta \,}
θ
=
sec
−
1
x
5
{\displaystyle \theta =\sec ^{-1}{\frac {x}{5}}\,}
Step 3 - Substituting Identities into Integral
∫
x
2
−
25
x
d
x
{\displaystyle \int {\frac {\sqrt {x^{2}-25}}{x}}dx\,}
=
∫
25
tan
2
θ
5
sec
θ
5
sec
tan
θ
d
θ
{\displaystyle =\int {\frac {\sqrt {25\tan ^{2}\theta }}{5\sec \theta }}\ 5\sec \tan \theta \,d\theta \,}
=
∫
5
tan
θ
5
sec
θ
5
sec
tan
θ
d
θ
{\displaystyle =\int {\frac {5\tan \theta }{5\sec \theta }}\ 5\sec \tan \theta \,d\theta \,}
=
∫
5
tan
θ
.
tan
θ
d
θ
{\displaystyle =\int 5\tan \theta \,.\,\tan \theta \,d\theta \,}
=
5
∫
tan
2
θ
d
θ
{\displaystyle =5\int \tan ^{2}\theta \,d\theta \,}
=
5
∫
(
sec
2
θ
−
1
)
d
θ
{\displaystyle =5\int (\sec ^{2}\theta -1)\,d\theta \,}
=
5
(
tan
θ
−
θ
)
+
C
{\displaystyle =5(\tan \theta -\theta )+C\,}
=
5
tan
θ
−
5
θ
+
C
{\displaystyle =5\tan \theta -5\theta +C\,}
Step 5 - Final Substitution of
θ
{\displaystyle \theta \,}
∫
x
2
−
25
x
d
x
{\displaystyle \int {\frac {\sqrt {x^{2}-25}}{x}}dx\,}
=
5
.
x
2
−
25
5
−
5
sec
−
1
x
5
+
C
{\displaystyle =5\,.\,{\frac {\sqrt {x^{2}-25}}{5}}-5\sec ^{-1}{\frac {x}{5}}+C\,}
=
x
2
−
25
−
5
sec
−
1
x
5
+
C
{\displaystyle ={\sqrt {x^{2}-25}}-5\sec ^{-1}{\frac {x}{5}}+C\,}